A igualdade entre razões denomina-se proporção.
Os números a, b, c e d, todos diferentes de zero, formam nesta ordem, uma proporção se, e somente se, a razão a : b for igual à razão c : d.
Indicamos esta proporção por:
Chamamos aos termos a e d de extremos e aos termos b e c chamamos de meios.
Veja que a razão de 10 para 5 é igual a 2 (10 : 5 = 2).
A razão de 14 para 7 também é igual a 2 (14 : 7 = 2).
Podemos então afirma que estas razões são iguais e que a igualdade abaixo representa uma proporção:
Lê-se a proporção acima da seguinte forma:
"10 está para 5, assim como 14 está para 7".
Colegio: Elizabeth souza serie:6ª ano 7ª professor: Luciano Reis Alunas: Lorena Batista e Lais Matos
segunda-feira, 4 de outubro de 2010
causas da evasão escolar
A evasão escolar ocorre quando o aluno deixa de frequentar a aula, caracterizando o abandono da escola durante o ano letivo.
No Brasil, a evasão escolar é um grande desafio para as escolas, pais e para o sistema educacional. Segundo dados do INEP (Instituto Nacional de Estudos e Pesquisas Anísio Teixeira), de 100 alunos que ingressam na escola na 1ª série, apenas 5 concluem o ensino fundamental, ou seja, apenas 5 terminam a 8ª série (IBGE, 2007).
Em 2007, 4,8% dos alunos matriculados no Ensino Fundamental (1ª a 8ª séries/1º ao 9º ano) abandonaram a escola. Embora o índice pareça pequeno, corresponde a quase um milhão e meio de alunos. No mesmo ano, 13,2% dos alunos que cursavam o Ensino Médio abandonaram a escola, o que corresponde a pouco mais de um milhão de alunos. Muitos desses alunos retornarão à escola, mas em uma incômoda condição de defasagem idade/série, o que pode causar conflitos e possivelmente nova evasão.
No Brasil, a evasão escolar é um grande desafio para as escolas, pais e para o sistema educacional. Segundo dados do INEP (Instituto Nacional de Estudos e Pesquisas Anísio Teixeira), de 100 alunos que ingressam na escola na 1ª série, apenas 5 concluem o ensino fundamental, ou seja, apenas 5 terminam a 8ª série (IBGE, 2007).
Em 2007, 4,8% dos alunos matriculados no Ensino Fundamental (1ª a 8ª séries/1º ao 9º ano) abandonaram a escola. Embora o índice pareça pequeno, corresponde a quase um milhão e meio de alunos. No mesmo ano, 13,2% dos alunos que cursavam o Ensino Médio abandonaram a escola, o que corresponde a pouco mais de um milhão de alunos. Muitos desses alunos retornarão à escola, mas em uma incômoda condição de defasagem idade/série, o que pode causar conflitos e possivelmente nova evasão.
evasão escolar
São vários os fatores que levam a evasão escolar. Ensino mal aplicado através de metodologias inadequadas, mal preparo do professor, problemas sociais, descaso governamental. O fato é, até quando vamos ficar parados sem fazer nada? Onde quer que se olhe em todo o Brasil você vê o que a falta do ensino e da oportunidade fazem com alguns cidadãos. Pessoas passando fome, a violência cada vez aumentando mais e isso tudo sem sombra de dúvida está relacionada à educação no Brasil. O mais grave nisso tudo é percebermos que o descaso das autoridades competentes para esse assunto é um absurdo. Cada vez mais fica claro que o Governo, a elite, quer manter esse padrão de controle sobre os ignorantes e sobre um povo sem voz, sem educação para poder sim ter suas próprias opiniões e se extinguir da submissão total. Para os governantes a falta de educação na população é na verdade um controle remoto, e através dele controla seu próprio poder.
quarta-feira, 29 de setembro de 2010
razão
Razão
Chama-se de razão entre dois números racionais a e b, com b ¹ 0, ao quociente entre eles. Indica-se a razão de a para b por a/b ou a : b.
Exemplo:
Na sala da 6ª B de um colégio há 20 rapazes e 25 moças. Encontre a razão entre o número de rapazes e o número de moças. (lembrando que razão é divisão)

Voltando ao exercício anterior, vamos encontrar a razão entre o número de moças e rapazes.

Lendo Razões

Chama-se de razão entre dois números racionais a e b, com b ¹ 0, ao quociente entre eles. Indica-se a razão de a para b por a/b ou a : b.
Exemplo:
Na sala da 6ª B de um colégio há 20 rapazes e 25 moças. Encontre a razão entre o número de rapazes e o número de moças. (lembrando que razão é divisão)

Voltando ao exercício anterior, vamos encontrar a razão entre o número de moças e rapazes.

Lendo Razões

quadrilatero
Quadrilátero
Definição:
Quadrilátero é um polígono de quatro lados.
 Quadrilátero ABCD
Quadrilátero ABCD
Em um quadrilátero, dois lados ou dois ângulos não-consecutivos são chamados opostos.


Quadrilátero ABCD
Vértices: A, B, C, e D.
Lados:
Diagonais:
Ângulos internos ou ângulos do
quadrilátero ABCD:
Observações
1.
Todo quadrilátero tem duas diagonais.
2.
O perímetro de um quadrilátero ABCD é a soma das medidas de seus lados, ou seja: AB + BC + CD + DA.
Côncavos e Convexos
Os quadriláteros podem ser convexos ou côncavos.
Um quadrilátero é convexo quando a reta que une dois vértices consecutivos não encontra o lado formado pelos dois outros vértices.
 Quadrilátero convexo
Quadrilátero convexo
 Quadrilátero côncavo
Quadrilátero côncavo
Definição:
Quadrilátero é um polígono de quatro lados.
 Quadrilátero ABCD
Quadrilátero ABCDEm um quadrilátero, dois lados ou dois ângulos não-consecutivos são chamados opostos.


Quadrilátero ABCD
Vértices: A, B, C, e D.
Lados:
Diagonais:
Ângulos internos ou ângulos do
quadrilátero ABCD:
Observações
1.
Todo quadrilátero tem duas diagonais.
2.
O perímetro de um quadrilátero ABCD é a soma das medidas de seus lados, ou seja: AB + BC + CD + DA.
Côncavos e Convexos
Os quadriláteros podem ser convexos ou côncavos.
Um quadrilátero é convexo quando a reta que une dois vértices consecutivos não encontra o lado formado pelos dois outros vértices.
 Quadrilátero convexo
Quadrilátero convexo Quadrilátero côncavo
Quadrilátero côncavo

O é o vértice dos
ângulos m, n, r e d
Analisando a figura notamos que, m e n são ângulos opostos pelo vértice, o mesmo acontece com os ângulos r e d.
Os ângulos opostos pelo vértice são ângulos congruentes (iguais).
Logo:
m = n e r = d
Observamos também que:
m + r = 180º, m + d = 180º, n + r = 180º, n + d = 180º
Exercícios resolvidos:
1. Vamos determinar os valores de a nas figuras seguintes:

a = 45°
São ângulos opostos pelo vértice, logo são ângulo iguais.
ÂNGULOS COMPLEMENTARES E ÂNGULOS SUPLEMENTARES
Observe os exemplos de ângulos consecutivos vistos anteriormente e verifique que:
ÂNGULOS ADJACENTES

Os ângulos AÔC e AÔB possuem pontos internos comuns

Os ângulos AÔC e AÔB possuem pontos internos comuns
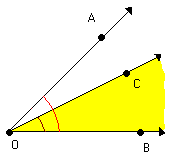
Os ângulos CÔB e AÔB possuem pontos internos comuns
Verifique que os ângulos AÔC e CÔB são consecutivos e não possuem pontos internos comuns. Por isso eles são denominados ângulos adjacentes.
Dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns.
Observação:
Duas retas concorrentes determinam vários ângulos adjacentes. Exemplos:


ÂNGULOS ADJACENTES

Os ângulos AÔC e AÔB possuem pontos internos comuns

Os ângulos AÔC e AÔB possuem pontos internos comuns

Os ângulos CÔB e AÔB possuem pontos internos comuns
Verifique que os ângulos AÔC e CÔB são consecutivos e não possuem pontos internos comuns. Por isso eles são denominados ângulos adjacentes.
Dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns.
Observação:
Duas retas concorrentes determinam vários ângulos adjacentes. Exemplos:


Multiplicação e divisão com angulos
> Multiplicação
40° 25' 32"
x 3
___________
120°75' 96"
120°76' 36"
121°16' 36"
96"-60"=36
76'-60=16'
> Divisão
40:3=13° 20
31° 15'=1° 25'
40° 25' 32"
x 3
___________
120°75' 96"
120°76' 36"
121°16' 36"
96"-60"=36
76'-60=16'
> Divisão
40:3=13° 20
31° 15'=1° 25'
Adição e Subtração com Ângulos
Adição
Dado os ângulos de 6º 25’ 36” e 4º 40’ 30”, a soma entre eles é:

O resultado da soma é 10º 65’ 66”, porém podemos apresentar o resultado de uma outra forma. Acompanhe a demonstração:
No ângulo de medida 10º 65’ 66”, temos que 65’ = 60’ + 5’ = 1º + 5’ e 66” = 60” + 6” = 1’ + 6”. Dessa forma, 10º 65’ 66” = 11º 6’ 6”.

Subtração
Dados os ângulos 54º 16’ 32” e 27º 18’ 40”, a subtração entre eles é:

Observe que existem valores no minuendo que são menores dos que os valores do subtraendo, quando isso acontece na subtração temos que tirar do valor da esquerda completando o que está menor.
Ao retirarmos 1’ de 16’ ficaremos com 15’, sendo que 1’ = 60” o qual deve ser somado a 32” resultando em 92”.
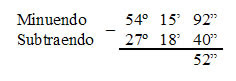
Agora devemos retirar 1º de 54º que será igual à 53º, considerando que 1º = 60’, temos 60’ + 15’ = 75’. Portanto:

Agora devemos retirar 1º de 54º que será igual à 53º, considerando que 1º = 60’, temos 60’ + 15’ = 75’. Portanto:
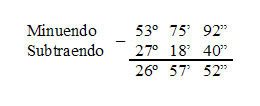
Dado os ângulos de 6º 25’ 36” e 4º 40’ 30”, a soma entre eles é:

O resultado da soma é 10º 65’ 66”, porém podemos apresentar o resultado de uma outra forma. Acompanhe a demonstração:
No ângulo de medida 10º 65’ 66”, temos que 65’ = 60’ + 5’ = 1º + 5’ e 66” = 60” + 6” = 1’ + 6”. Dessa forma, 10º 65’ 66” = 11º 6’ 6”.

Subtração
Dados os ângulos 54º 16’ 32” e 27º 18’ 40”, a subtração entre eles é:

Observe que existem valores no minuendo que são menores dos que os valores do subtraendo, quando isso acontece na subtração temos que tirar do valor da esquerda completando o que está menor.
Ao retirarmos 1’ de 16’ ficaremos com 15’, sendo que 1’ = 60” o qual deve ser somado a 32” resultando em 92”.
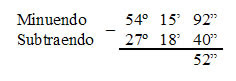
Agora devemos retirar 1º de 54º que será igual à 53º, considerando que 1º = 60’, temos 60’ + 15’ = 75’. Portanto:

Agora devemos retirar 1º de 54º que será igual à 53º, considerando que 1º = 60’, temos 60’ + 15’ = 75’. Portanto:
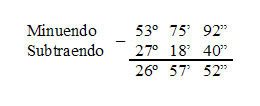
Operações com medidas de ângulos
simbolos:
1°_um grau
1' minuto
1''seguundos
Transformando unidades:
15° 12'--minutos
15x60=900
900'+12'=912'
120'--Graus
120:60=2°
180"--minutos
180:60=3°
resultado
Graus- minutos-segundos-multiplicar por 60
segundos-minutos-Graus- dividir por 60
Os ângulos podem ser somados, multiplicados, subtraídos e divididos. Para fazer isso, no entanto, é necessário levar em conta uma característica específica: suas sub-unidades são os minutos e os segundos, e muitas vezes é necessário fazer transformações com medidas de ângulos durante essas operações.
Quando você efetua uma soma de números decimais e quando a soma das unidades chega a dez ou mais, você "leva 1" à casa das dezenas. O mesmo vale para as dezenas ("vai 1" na casa das centenas), e assim por diante.
No caso dos ângulos é a mesma coisa: quando os minutos chegarem a 60 ou mais, você adiciona "1" na casa dos graus.


somando-se os minutos, obtém-se:

Como o resultado excedeu os 60', ficam 12' na casa dos minutos e vão 60' para a casa dos graus. 60' = 1º, então, você leva 1º para a casa dos minutos.

O mesmo vale para os segundos:

sobram 24" e vai 1:

somam-se agora os minutos:

Sobram 13' e vai 1º.

Exemplo
Veja outro exemplo da operação, e você entenderá melhor como ela funciona:


sobram 3'' e vai 1:

somam-se agora os minutos:

sobram 14' e vai 1°:

1°_um grau
1' minuto
1''seguundos
Transformando unidades:
15° 12'--minutos
15x60=900
900'+12'=912'
120'--Graus
120:60=2°
180"--minutos
180:60=3°
resultado
Graus- minutos-segundos-multiplicar por 60
segundos-minutos-Graus- dividir por 60
Os ângulos podem ser somados, multiplicados, subtraídos e divididos. Para fazer isso, no entanto, é necessário levar em conta uma característica específica: suas sub-unidades são os minutos e os segundos, e muitas vezes é necessário fazer transformações com medidas de ângulos durante essas operações.
Quando você efetua uma soma de números decimais e quando a soma das unidades chega a dez ou mais, você "leva 1" à casa das dezenas. O mesmo vale para as dezenas ("vai 1" na casa das centenas), e assim por diante.
No caso dos ângulos é a mesma coisa: quando os minutos chegarem a 60 ou mais, você adiciona "1" na casa dos graus.


somando-se os minutos, obtém-se:

Como o resultado excedeu os 60', ficam 12' na casa dos minutos e vão 60' para a casa dos graus. 60' = 1º, então, você leva 1º para a casa dos minutos.

O mesmo vale para os segundos:

sobram 24" e vai 1:

somam-se agora os minutos:

Sobram 13' e vai 1º.

Exemplo
Veja outro exemplo da operação, e você entenderá melhor como ela funciona:


sobram 3'' e vai 1:

somam-se agora os minutos:

sobram 14' e vai 1°:

quarta-feira, 4 de agosto de 2010
Operações com medidas de ângulos
Adição de graus, minutos e segundos
Os ângulos podem ser somados, multiplicados, subtraídos e divididos. Para fazer isso, no entanto, é necessário levar em conta uma característica específica: suas sub-unidades são os minutos e os segundos, e muitas vezes é necessário fazer transformações com medidas de ângulos durante essas operações.
Quando você efetua uma soma de números decimais e quando a soma das unidades chega a dez ou mais, você "leva 1" à casa das dezenas. O mesmo vale para as dezenas ("vai 1" na casa das centenas), e assim por diante.
No caso dos ângulos é a mesma coisa: quando os minutos chegarem a 60 ou mais, você adiciona "1" na casa dos graus.
Veja este exemplo:
Folha Imagem
somando-se os minutos, obtém-se:
Folha Imagem
Como o resultado excedeu os 60', ficam 12' na casa dos minutos e vão 60' para a casa dos graus. 60' = 1º, então, você leva 1º para a casa dos minutos.
Folha Imagem
O mesmo vale para os segundos:
Folha Imagem
sobram 24" e vai 1:
Folha Imagem
somam-se agora os minutos:
Folha Imagem
Sobram 13' e vai 1º.
Folha Imagem
Exemplo
Veja outro exemplo da operação, e você entenderá melhor como ela funciona:
Folha Imagem
Folha Imagem
sobram 3'' e vai 1:
Folha Imagem
somam-se agora os minutos:
Folha Imagem
sobram 14' e vai 1°:
EXERCIICOS sobre operações com medidas de angulo?
determine::
a) (46° 48' 54'') : 2 =
b)(31° 32' 45'' ) : 3 =
c)(52° 63' 42'') : 5 =
d)45° : 2 =
a) (46° 48' 54'') : 2 = Divide-se normalmente
23° 24' 27''
b)(31° 32' 45'' ) : 3 Vc deve transformar os valores para que a divisão dê exata. Primeiro vc passa os 2' para a casa dos segundos - lembrando de somar 60 quantas vezes vc tirou da casa anterior)
31° 30' 165'' ( 2' equivale a 120" somado com os 45" tem-se 165")
Vc devefazer isso com os graus passando para minutos, aplicando a mesma regra)
30° 90' 165'' ( Como 1 grau vale 60 min) Agora vc pode dividir normalmente:
30° 90' 165'' : 3 = 10° 30' 55''
c) (52° 63' 42'') : 5
d) 45° : 2 = desmembra o 45° em graus e minutos:
44° 60' : 2 = depois divide normalmente
Adição de graus, minutos e segundos
Os ângulos podem ser somados, multiplicados, subtraídos e divididos. Para fazer isso, no entanto, é necessário levar em conta uma característica específica: suas sub-unidades são os minutos e os segundos, e muitas vezes é necessário fazer transformações com medidas de ângulos durante essas operações.
Quando você efetua uma soma de números decimais e quando a soma das unidades chega a dez ou mais, você "leva 1" à casa das dezenas. O mesmo vale para as dezenas ("vai 1" na casa das centenas), e assim por diante.
No caso dos ângulos é a mesma coisa: quando os minutos chegarem a 60 ou mais, você adiciona "1" na casa dos graus.
Veja este exemplo:
Folha Imagem
somando-se os minutos, obtém-se:
Folha Imagem
Como o resultado excedeu os 60', ficam 12' na casa dos minutos e vão 60' para a casa dos graus. 60' = 1º, então, você leva 1º para a casa dos minutos.
Folha Imagem
O mesmo vale para os segundos:
Folha Imagem
sobram 24" e vai 1:
Folha Imagem
somam-se agora os minutos:
Folha Imagem
Sobram 13' e vai 1º.
Folha Imagem
Exemplo
Veja outro exemplo da operação, e você entenderá melhor como ela funciona:
Folha Imagem
Folha Imagem
sobram 3'' e vai 1:
Folha Imagem
somam-se agora os minutos:
Folha Imagem
sobram 14' e vai 1°:
EXERCIICOS sobre operações com medidas de angulo?
determine::
a) (46° 48' 54'') : 2 =
b)(31° 32' 45'' ) : 3 =
c)(52° 63' 42'') : 5 =
d)45° : 2 =
a) (46° 48' 54'') : 2 = Divide-se normalmente
23° 24' 27''
b)(31° 32' 45'' ) : 3 Vc deve transformar os valores para que a divisão dê exata. Primeiro vc passa os 2' para a casa dos segundos - lembrando de somar 60 quantas vezes vc tirou da casa anterior)
31° 30' 165'' ( 2' equivale a 120" somado com os 45" tem-se 165")
Vc devefazer isso com os graus passando para minutos, aplicando a mesma regra)
30° 90' 165'' ( Como 1 grau vale 60 min) Agora vc pode dividir normalmente:
30° 90' 165'' : 3 = 10° 30' 55''
c) (52° 63' 42'') : 5
d) 45° : 2 = desmembra o 45° em graus e minutos:
44° 60' : 2 = depois divide normalmente
Ângulos
O ÂNGULO E SEUS ELEMENTOS
Duas semi-retas que não estejam contidas na mesma reta, e que tenham a mesma origem, dividem o plano em duas regiões: uma convexa e outra não-convexa.
Cada uma dessas regiões, junto com as semi-retas, forma um ângulo. Assim, as duas semi-retas determinam dois ângulos:
Todo ângulo possui dois lados e um vértice. Os lados são as semi-retas que determinam. O vértice é a origem comum dessas semi-retas.
O ângulo convexo, de vértice O e lados , é indicado por: AÔB, BÔA ou Ô.
Ângulos
Observe agora dois casos em que as semi-retas de mesma origem estão contidas na mesma reta. Nesses casos, formam-se também ângulos.
* As semi-retas coincidem. Temos aí o ângulo nulo e o ângulo de uma volta.
* As semi-retas não coincidem. Temos aí dois ângulos rasos ou de meia-volta.
Podemos, então, estabelecer que:
Ângulo é a região do plano limitada por duas semi-retas que têm a mesma origem.
MEDIDA DE UM ÂNGULO
A medida de um ângulo é dada pela medida de sua abertura. A unidade padrão de medida de um ângulo é o grau, cujo símbolo é º.
Tomando um ângulo raso ou de meia-volta e dividindo-o em 180 partes iguais, determinamos 180 ângulos de mesma medida. Cada um desses ângulos representa um ângulo de 1º grau (1º).
Para medir ângulos utilizamos um instrumento denominado transferidor. O transferidor já vem graduado com divisões de 1º em 1º. Existem dois tipos de transferidor: Transferidor de 180º e de 360º.
O grau compreende os submúltiplos:
* O minuto corresponde a do grau. Indica-se um minuto por 1'.
1º=60'
* O segundo corresponde a do minuto. Indica-se um segundo por 1''.
1'=60''
Logo, podemos concluir que:
1º = 60'.60 = 3.600''
Quando um ângulo é medido em graus, minutos e segundos, estamos utilizando o sistema sexagesimal.
Ângulos
Como medir um ângulo, utilizando o transferidor
Observe a seqüência
* O centro O do transferidor deve ser colocado sobre o vértice do ângulo.
* A linha horizontal que passa pelo centro deve coincidir com uma das semi-retas do ângulo .
* Verificamos a medida da escala em que passa a outra semi-reta .
Leitura de um ângulo
Observe as seguintes indicações de ângulos e suas respectivas leituras:
15º (lê-se "15 graus'')
45º50' (lê-se ''45 graus e 50 minutos'')
30º48'36'' (lê-se ''30 graus, 48 minutos e 36 segundos'')
Observações
Além do transferidor, existem outros instrumentos que medem ângulos com maior precisão. Como exemplos temos o teodolito, utilizado na agrimensura, e o sextante, utilizado em navegação.
A representação da medida de um ângulo pode também ser feita através de uma letra minúscula ou de um número.
Um ângulo raso ou de meia-volta mede 180º.
O ângulo de uma volta mede 360º.
Questões envolvendo medidas de ângulos
Observe a resolução das questões abaixo:
* Determine a medida do ângulo AÔB na figura:
Solução
Medida de AÔB = x
Medida de BÔC = 105º
Como m ( AÔC) é 180º, pois é um ângulo raso, temos:
m (AÔB) + m (BÔC) = m (AÔC)
x + 105º = 180º
x = 180º - 105º
x = 75º
Logo, a medida de AÔB é 75º.
* Determine a medida do 6angulo não-convexo na figura:
Solução
Verificamos que o ângulo não-convexo na figura (x) e o ângulo convexo (50º) formam, juntos, um ângulo de uma volta, que mede 360º. Assim:
x + 50º = 360º
x = 360º - 50º
x = 310º
Logo, o valor do ângulo não-convexo é 310º.
O ÂNGULO E SEUS ELEMENTOS
Duas semi-retas que não estejam contidas na mesma reta, e que tenham a mesma origem, dividem o plano em duas regiões: uma convexa e outra não-convexa.
Cada uma dessas regiões, junto com as semi-retas, forma um ângulo. Assim, as duas semi-retas determinam dois ângulos:
Todo ângulo possui dois lados e um vértice. Os lados são as semi-retas que determinam. O vértice é a origem comum dessas semi-retas.
O ângulo convexo, de vértice O e lados , é indicado por: AÔB, BÔA ou Ô.
Ângulos
Observe agora dois casos em que as semi-retas de mesma origem estão contidas na mesma reta. Nesses casos, formam-se também ângulos.
* As semi-retas coincidem. Temos aí o ângulo nulo e o ângulo de uma volta.
* As semi-retas não coincidem. Temos aí dois ângulos rasos ou de meia-volta.
Podemos, então, estabelecer que:
Ângulo é a região do plano limitada por duas semi-retas que têm a mesma origem.
MEDIDA DE UM ÂNGULO
A medida de um ângulo é dada pela medida de sua abertura. A unidade padrão de medida de um ângulo é o grau, cujo símbolo é º.
Tomando um ângulo raso ou de meia-volta e dividindo-o em 180 partes iguais, determinamos 180 ângulos de mesma medida. Cada um desses ângulos representa um ângulo de 1º grau (1º).
Para medir ângulos utilizamos um instrumento denominado transferidor. O transferidor já vem graduado com divisões de 1º em 1º. Existem dois tipos de transferidor: Transferidor de 180º e de 360º.
O grau compreende os submúltiplos:
* O minuto corresponde a do grau. Indica-se um minuto por 1'.
1º=60'
* O segundo corresponde a do minuto. Indica-se um segundo por 1''.
1'=60''
Logo, podemos concluir que:
1º = 60'.60 = 3.600''
Quando um ângulo é medido em graus, minutos e segundos, estamos utilizando o sistema sexagesimal.
Ângulos
Como medir um ângulo, utilizando o transferidor
Observe a seqüência
* O centro O do transferidor deve ser colocado sobre o vértice do ângulo.
* A linha horizontal que passa pelo centro deve coincidir com uma das semi-retas do ângulo .
* Verificamos a medida da escala em que passa a outra semi-reta .
Leitura de um ângulo
Observe as seguintes indicações de ângulos e suas respectivas leituras:
15º (lê-se "15 graus'')
45º50' (lê-se ''45 graus e 50 minutos'')
30º48'36'' (lê-se ''30 graus, 48 minutos e 36 segundos'')
Observações
Além do transferidor, existem outros instrumentos que medem ângulos com maior precisão. Como exemplos temos o teodolito, utilizado na agrimensura, e o sextante, utilizado em navegação.
A representação da medida de um ângulo pode também ser feita através de uma letra minúscula ou de um número.
Um ângulo raso ou de meia-volta mede 180º.
O ângulo de uma volta mede 360º.
Questões envolvendo medidas de ângulos
Observe a resolução das questões abaixo:
* Determine a medida do ângulo AÔB na figura:
Solução
Medida de AÔB = x
Medida de BÔC = 105º
Como m ( AÔC) é 180º, pois é um ângulo raso, temos:
m (AÔB) + m (BÔC) = m (AÔC)
x + 105º = 180º
x = 180º - 105º
x = 75º
Logo, a medida de AÔB é 75º.
* Determine a medida do 6angulo não-convexo na figura:
Solução
Verificamos que o ângulo não-convexo na figura (x) e o ângulo convexo (50º) formam, juntos, um ângulo de uma volta, que mede 360º. Assim:
x + 50º = 360º
x = 360º - 50º
x = 310º
Logo, o valor do ângulo não-convexo é 310º.
Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas.
Quando terminamos a resolução de um sistema de inequações chegamos a um conjunto solução, esse é composto por possíveis valores que x deverá assumir para que exista o sistema.
Para chegamos a esse conjunto solução devemos achar o conjunto solução de cada inequação envolvida no sistema, a partir daí fazermos a intersecção dessas soluções.
O conjunto formado pela intesecção chamamos de CONJUNTO SOLUÇÃO do sistema.
Veja alguns exemplos de sistema de inequação do 1º grau:
Vamos achar a solução de cada inequação.
4x + 4 ≤ 0
4x ≤ - 4
x ≤ - 4 : 4
x ≤ - 1
S1 = {x R | x ≤ - 1}
Fazendo o cálculo da segunda inequação temos:
x + 1 ≤ 0
x ≤ - 1
A “bolinha” é fechada, pois o sinal da inequação é igual.
S2 = { x R | x ≤ - 1}
Calculando agora o CONJUTO SOLUÇÃO da inequação temos:
S = S1 ∩ S2
Portanto:
S = { x R | x ≤ - 1} ou S = ] - ∞ ; -1]
Em primeiro lugar devemos calcular o conjunto solução de cada inequação.
3x + 1 > 0
3x > -1
x > -1
3
A “bolinha” é aberta, pois o sinal da inequação não é igual.
Calculamos agora o conjunto solução da outra solução.
5x – 4 ≤ 0
5x ≤ 4
x ≤ 4
5
Agora podemos calcular o CONJUNTO SOLUÇÃO da inequação, assim temos:
S = S1 ∩ S2
Portanto:
S = { x R | -1 < x ≤ 4} ou S = ] -1 ; 4]
3 5 3 5
Devemos organizar o sistema antes de resolvê-lo, veja como fica:
Calculando o conjunto solução de cada inequação temos:
10x – 2 ≥ 4
10x ≥ 4 + 2
10x ≥ 6
x ≥ 6
10
x ≥ 3
5
6x + 8 < 2x + 10
6x -2x < 10 – 8
4x < 2
x < 2
4
x < 1
2
Podemos calcular o CONJUNTO SOLUÇÃO da inequação, assim temos:
S = S1 ∩ S2
Observando a solução veremos que não há intersecção, então o conjunto solução desse sistema inequação, será:
S =
Quando terminamos a resolução de um sistema de inequações chegamos a um conjunto solução, esse é composto por possíveis valores que x deverá assumir para que exista o sistema.
Para chegamos a esse conjunto solução devemos achar o conjunto solução de cada inequação envolvida no sistema, a partir daí fazermos a intersecção dessas soluções.
O conjunto formado pela intesecção chamamos de CONJUNTO SOLUÇÃO do sistema.
Veja alguns exemplos de sistema de inequação do 1º grau:
Vamos achar a solução de cada inequação.
4x + 4 ≤ 0
4x ≤ - 4
x ≤ - 4 : 4
x ≤ - 1
S1 = {x R | x ≤ - 1}
Fazendo o cálculo da segunda inequação temos:
x + 1 ≤ 0
x ≤ - 1
A “bolinha” é fechada, pois o sinal da inequação é igual.
S2 = { x R | x ≤ - 1}
Calculando agora o CONJUTO SOLUÇÃO da inequação temos:
S = S1 ∩ S2
Portanto:
S = { x R | x ≤ - 1} ou S = ] - ∞ ; -1]
Em primeiro lugar devemos calcular o conjunto solução de cada inequação.
3x + 1 > 0
3x > -1
x > -1
3
A “bolinha” é aberta, pois o sinal da inequação não é igual.
Calculamos agora o conjunto solução da outra solução.
5x – 4 ≤ 0
5x ≤ 4
x ≤ 4
5
Agora podemos calcular o CONJUNTO SOLUÇÃO da inequação, assim temos:
S = S1 ∩ S2
Portanto:
S = { x R | -1 < x ≤ 4} ou S = ] -1 ; 4]
3 5 3 5
Devemos organizar o sistema antes de resolvê-lo, veja como fica:
Calculando o conjunto solução de cada inequação temos:
10x – 2 ≥ 4
10x ≥ 4 + 2
10x ≥ 6
x ≥ 6
10
x ≥ 3
5
6x + 8 < 2x + 10
6x -2x < 10 – 8
4x < 2
x < 2
4
x < 1
2
Podemos calcular o CONJUNTO SOLUÇÃO da inequação, assim temos:
S = S1 ∩ S2
Observando a solução veremos que não há intersecção, então o conjunto solução desse sistema inequação, será:
S =
sexta-feira, 9 de julho de 2010
A Matemática é uma das disciplinas mais importantes para qualquer aluno. Escrevo isto, porque, também é desde sempre uma disciplina que os alunos acham bastante difícil e árida e com pouca relevância para a sua vida diária, dizem eles. Venho aqui defender a dama da Matemática. Também já fui aluno, também já tive dificuldades com ela, mas aprendi a gostar da matemática e a considerá-la absolutamente fundamental para o desenvolvimento mental do indivíduo.
E porquê, perguntam vocês, é a Matemática assim tão importante?
No meu ponto de vista, a grande mais vaia da Matemática não é apenas a simples aritmética do dia a dia, mas sim, o desenvolvimento do raciocínio. Grande parte da Matemática assenta em deduções lógicas, dependentes umas das outras. Devemos ser capazes de ‘partir’ um problema em passos lógicos e resolvê-lo passo a passo, usando técnicas e teoremas que muitas vezes são o resultado de anos de aprendizagem. O raciocino que temos de desenvolver para a resolução dos problemas Matemáticos pode, e deve, ser utilizado em muitas outras áreas do conhecimento e da nossa vida e é a grande mais valia que esta disciplina traz ao comum dos cidadãos
E porquê, perguntam vocês, é a Matemática assim tão importante?
No meu ponto de vista, a grande mais vaia da Matemática não é apenas a simples aritmética do dia a dia, mas sim, o desenvolvimento do raciocínio. Grande parte da Matemática assenta em deduções lógicas, dependentes umas das outras. Devemos ser capazes de ‘partir’ um problema em passos lógicos e resolvê-lo passo a passo, usando técnicas e teoremas que muitas vezes são o resultado de anos de aprendizagem. O raciocino que temos de desenvolver para a resolução dos problemas Matemáticos pode, e deve, ser utilizado em muitas outras áreas do conhecimento e da nossa vida e é a grande mais valia que esta disciplina traz ao comum dos cidadãos
quarta-feira, 7 de julho de 2010
sistema de duas equações do 1 grau com duas incóguinitas
Equações de primeiro grau com duas incógnitas
Seja x + y = 8 uma equação linear nas variáveis x e y, em que seu conjunto solução pertence a R X R.
Algumas de suas possíveis soluções são (5, 3); (– 2, 10) e (8, 0).
Observe que não há uma única solução. Na verdade, podemos encontrar um número infinito de soluções para esta equação.
Exemplo:
Acompanhe o seguinte exercício: a soma de dois números é 8 e sua diferença é 2. Que números são esses? Se x e y são esses números, as equações serão:
x + y = 8 (a soma é 8); x– y = 2 (a diferença é 2)
Esse tipo de situação em que aparece mais de uma equação recebe o nome de sistema de equações.
Podemos observar que essas equações têm uma solução em comum, isto é, que há um par de números (x,y) que fazem cumprir simultaneamente a igualdade numérica nas duas equações. Neste caso é (5, 3).
Para lembrar:
A solução de um sistema de equações é o conjunto de valores das incógnitas que, substituídas em todas as equações, as transformam em identidades.
Para lembrar:
Os sistemas de equações classificam-se em determinados, indeterminados e impossíveis ou incompatíveis, segundo tenham uma única solução, infinitas soluções ou não tenham nenhuma solução, respectivamente.
Sistema de equações
Um conjunto de m equações com n incógnitas recebe o nome de sistema linear de equações.
A solução do sistema é:
•
Um conjunto de pares ordenados, se o sistema tiver duas incógnitas;
•
Um conjunto de ternas ordenadas, se o sistema tiver três incógnitas, e assim sucessivamente. São soluções, simultaneamente, das m equações; isto é, a solução do sistema é a interseção dos conjuntos solução das equações.
O processo para encontrar a solução de um sistema de equações é conhecido como resolução simultânea.
Sistema de duas equações lineares
Exemplo:
Observe que, como a segunda equação só tem o x, podemos isolar a incógnita e achar seu valor.
O valor x = 4 pertence à solução do sistema, pois é a única solução da segunda equação.
Substituímos, agora, x por seu valor (4) na primeira equação do exemplo:
A solução do sistema de equações compõe-se dos valores:
x = 4 e y = 2
Podemos facilmente comprovar isso substituindo os valores achados no sistema inicial:
3 X 4 – 5 X 2 = 2, do qual obtemos 2 = 2
2 X 4 = 8, do qual obtemos 8 = 8
Métodos de resolução
Existem três métodos para resolver um sistema de equações com duas incógnitas:
•
Comparação
•
Substituição
•
Adição
É conveniente observar, antes de começar a resolução do sistema por um dos métodos acima, se alguma equação pode ser simplificada, o que facilitará a operação.
Resolução de um sistema de equações por comparação
Esse método consiste em:
•
Isolar uma mesma incógnita em cada equação.
•
Igualar as duas expressões.
•
Resolver a equação de primeiro grau assim obtida.
Exemplo:
Resolver, por este método, o seguinte sistema:
•
Escolhemos uma das incógnitas, x ou y, isolando-a em ambas as equações.
Optamos pela incógnita x.
Na primeira equação:
Na segunda equação:
x = 5 + 2y
Se a incógnita x pode ser expressa na forma (5 + 2y) e na forma, então essas duas expressões são iguais.
•
Portanto, vamos igualar as duas expressões obtidas:
•
Resolvemos agora a equação obtida:
Para achar o valor da outra incógnita, x, voltamos ao início do exemplo e, em qualquer das expressões onde o x aparece isolado, substituímos o valor de y por (– 1).
Substituímos esse valor na expressão mais simples:
x = 5 + 2yx = 5 + 2(– 1)x = 5 – 2x = 3
Observe que, se fizermos substituição igual de y na outra expressão, o resultado será o mesmo:
Seja x + y = 8 uma equação linear nas variáveis x e y, em que seu conjunto solução pertence a R X R.
Algumas de suas possíveis soluções são (5, 3); (– 2, 10) e (8, 0).
Observe que não há uma única solução. Na verdade, podemos encontrar um número infinito de soluções para esta equação.
Exemplo:
Acompanhe o seguinte exercício: a soma de dois números é 8 e sua diferença é 2. Que números são esses? Se x e y são esses números, as equações serão:
x + y = 8 (a soma é 8); x– y = 2 (a diferença é 2)
Esse tipo de situação em que aparece mais de uma equação recebe o nome de sistema de equações.
Podemos observar que essas equações têm uma solução em comum, isto é, que há um par de números (x,y) que fazem cumprir simultaneamente a igualdade numérica nas duas equações. Neste caso é (5, 3).
Para lembrar:
A solução de um sistema de equações é o conjunto de valores das incógnitas que, substituídas em todas as equações, as transformam em identidades.
Para lembrar:
Os sistemas de equações classificam-se em determinados, indeterminados e impossíveis ou incompatíveis, segundo tenham uma única solução, infinitas soluções ou não tenham nenhuma solução, respectivamente.
Sistema de equações
Um conjunto de m equações com n incógnitas recebe o nome de sistema linear de equações.
A solução do sistema é:
•
Um conjunto de pares ordenados, se o sistema tiver duas incógnitas;
•
Um conjunto de ternas ordenadas, se o sistema tiver três incógnitas, e assim sucessivamente. São soluções, simultaneamente, das m equações; isto é, a solução do sistema é a interseção dos conjuntos solução das equações.
O processo para encontrar a solução de um sistema de equações é conhecido como resolução simultânea.
Sistema de duas equações lineares
Exemplo:
Observe que, como a segunda equação só tem o x, podemos isolar a incógnita e achar seu valor.
O valor x = 4 pertence à solução do sistema, pois é a única solução da segunda equação.
Substituímos, agora, x por seu valor (4) na primeira equação do exemplo:
A solução do sistema de equações compõe-se dos valores:
x = 4 e y = 2
Podemos facilmente comprovar isso substituindo os valores achados no sistema inicial:
3 X 4 – 5 X 2 = 2, do qual obtemos 2 = 2
2 X 4 = 8, do qual obtemos 8 = 8
Métodos de resolução
Existem três métodos para resolver um sistema de equações com duas incógnitas:
•
Comparação
•
Substituição
•
Adição
É conveniente observar, antes de começar a resolução do sistema por um dos métodos acima, se alguma equação pode ser simplificada, o que facilitará a operação.
Resolução de um sistema de equações por comparação
Esse método consiste em:
•
Isolar uma mesma incógnita em cada equação.
•
Igualar as duas expressões.
•
Resolver a equação de primeiro grau assim obtida.
Exemplo:
Resolver, por este método, o seguinte sistema:
•
Escolhemos uma das incógnitas, x ou y, isolando-a em ambas as equações.
Optamos pela incógnita x.
Na primeira equação:
Na segunda equação:
x = 5 + 2y
Se a incógnita x pode ser expressa na forma (5 + 2y) e na forma, então essas duas expressões são iguais.
•
Portanto, vamos igualar as duas expressões obtidas:
•
Resolvemos agora a equação obtida:
Para achar o valor da outra incógnita, x, voltamos ao início do exemplo e, em qualquer das expressões onde o x aparece isolado, substituímos o valor de y por (– 1).
Substituímos esse valor na expressão mais simples:
x = 5 + 2yx = 5 + 2(– 1)x = 5 – 2x = 3
Observe que, se fizermos substituição igual de y na outra expressão, o resultado será o mesmo:
quinta-feira, 10 de junho de 2010
Primeira Aula
As equações do primeiro grau são aquelas que podem ser representadas sob a forma ax+b=0,em que a e b são constantes reais, com a diferente de 0, e x é a variável. A resolução desse tipo de equação é fundamentada nas propriedades da igualdade descritas a seguir.
Adicionando um mesmo número a ambos os membros de uma equação, ou subtraindo um mesmo número de ambos os membros, a igualdade se mantém.
Dividindo ou multiplicando ambos os membros de uma equação por um mesmo número não-nulo, a igualdade se mantém.
Exemplo:
Membros de uma equação
Numa equação a expressão situada à esquerda da igualdade é chamada de 1º membro da equação, e a expressão situada à direita da igualdade, de 2º membro da equação.
Exemplo: - 3x + 12 = 2x - 9
1º membro 2º membro
Cada uma das parcelas que compõem um membro de uma equação é chamada termo da equação.
4x – 9 = 1 – 2x
termos
Variável (ou incógnita) de uma equação:
Os elementos desconhecidos de uma equação são chamados de variáveis ou incógnitas.
Exemplos:
A equação x + 5 = 18 tem uma incógnita: x
A equação x – 3 = y + 2 tem duas incógnitas: x e y
A equação a² – 3b + c = 0 tem três incógnitas: a, b e c
Cada um dos valores que, colocados no lugar da incógnita, transformam a equação em uma sentença verdadeira é chamado de raiz da equação. Para verificarmos se um dado número é ou não raiz de uma equação, basta substituirmos a incógnita por esse número e observarmos se a sentença obtida é ou não verdadeira.
1º exemplo: verificar se três é raiz de 5x – 3 = 2x + 6
2º exemplo: verificar se -2 é raiz de x² – 3x = x – 6
O princípio aditivo e o princípio multiplicativo servem para facilitar o entendimento da solução de uma equação, mas para resolvê-la existe um método simples e prático que é o seguinte:
Resolver a equação 5x – 8 = 12 + x
Colocamos no primeiro membro os termos que apresentam variável, e no segundo membro os termos que não apresentam variável. Os termos que mudam de membro tem os sinais trocados.
5x – 8 = 12 + x
5x – x = 12 + 8
Calculamos a somas algebricas de cada termo.
4.x = 20
Quando se passa de um membro para o outro usa-se a operação inversa, ou seja, o que está multiplicando passa dividindo e o que está dividindo passa multiplicando. O que está adicinando passa subtraindo e o que está subtraindo passa adicionando. O número 4 no primeiro membro está multiplicando o x então ele passará dividindo no segundo membro.
Exercícios resolvidos:
1) Resolver a equação:
2( x + 5 ) - 3( 5 – x ) = 5
Nesse tipo de equação, devemos inicialmente, retirar os parênteses, aplicando a propriedade distributiva da multiplicação e a regra de eliminação de parênteses.
Para eliminar os denominadores multiplicamos todos os termos da equação pelo m.m.c. dos denominadores
Nessa equação, inicialmente reduzimos todas as frações ao mesmo denominador, e a seguir cancelamos esses denominadores
m.m.c ( 3, 2, 6 ) = 6
3, 2, 6 2
3, 1, 3 3
1, 1, 1 2 . 3 = 6
Adicionando um mesmo número a ambos os membros de uma equação, ou subtraindo um mesmo número de ambos os membros, a igualdade se mantém.
Dividindo ou multiplicando ambos os membros de uma equação por um mesmo número não-nulo, a igualdade se mantém.
Exemplo:
Membros de uma equação
Numa equação a expressão situada à esquerda da igualdade é chamada de 1º membro da equação, e a expressão situada à direita da igualdade, de 2º membro da equação.
Exemplo: - 3x + 12 = 2x - 9
1º membro 2º membro
Cada uma das parcelas que compõem um membro de uma equação é chamada termo da equação.
4x – 9 = 1 – 2x
termos
Variável (ou incógnita) de uma equação:
Os elementos desconhecidos de uma equação são chamados de variáveis ou incógnitas.
Exemplos:
A equação x + 5 = 18 tem uma incógnita: x
A equação x – 3 = y + 2 tem duas incógnitas: x e y
A equação a² – 3b + c = 0 tem três incógnitas: a, b e c
Cada um dos valores que, colocados no lugar da incógnita, transformam a equação em uma sentença verdadeira é chamado de raiz da equação. Para verificarmos se um dado número é ou não raiz de uma equação, basta substituirmos a incógnita por esse número e observarmos se a sentença obtida é ou não verdadeira.
1º exemplo: verificar se três é raiz de 5x – 3 = 2x + 6
2º exemplo: verificar se -2 é raiz de x² – 3x = x – 6
O princípio aditivo e o princípio multiplicativo servem para facilitar o entendimento da solução de uma equação, mas para resolvê-la existe um método simples e prático que é o seguinte:
Resolver a equação 5x – 8 = 12 + x
Colocamos no primeiro membro os termos que apresentam variável, e no segundo membro os termos que não apresentam variável. Os termos que mudam de membro tem os sinais trocados.
5x – 8 = 12 + x
5x – x = 12 + 8
Calculamos a somas algebricas de cada termo.
4.x = 20
Quando se passa de um membro para o outro usa-se a operação inversa, ou seja, o que está multiplicando passa dividindo e o que está dividindo passa multiplicando. O que está adicinando passa subtraindo e o que está subtraindo passa adicionando. O número 4 no primeiro membro está multiplicando o x então ele passará dividindo no segundo membro.
Exercícios resolvidos:
1) Resolver a equação:
2( x + 5 ) - 3( 5 – x ) = 5
Nesse tipo de equação, devemos inicialmente, retirar os parênteses, aplicando a propriedade distributiva da multiplicação e a regra de eliminação de parênteses.
Para eliminar os denominadores multiplicamos todos os termos da equação pelo m.m.c. dos denominadores
Nessa equação, inicialmente reduzimos todas as frações ao mesmo denominador, e a seguir cancelamos esses denominadores
m.m.c ( 3, 2, 6 ) = 6
3, 2, 6 2
3, 1, 3 3
1, 1, 1 2 . 3 = 6
segunda-feira, 7 de junho de 2010
Assinar:
Postagens (Atom)


